動態規劃概述
动态规划(Dynamic Programming)
将一个问题拆成几个子问题,分别求解这些子问题,即可推断出大问题的解。
如何判断一个问题能否使用DP解决呢?
能将大问题拆成几个小问题,且满足无后效性、最优子结构性质。
即是确定 DP状态
最优子结构:
将原有问题化分为一个个子问题,即为子结构。而对于每一个子问题,其最优值均由「更小规模的子问题的最优值」推导而来,即为最优子结构。
因此「DP 状态」设置之前,需要将原有问题划分为一个个子问题,且需要确保子问题的最优值由「更小规模子问题的最优值」推出,此时子问题的最优值即为「DP 状态」的定义。
无后效性:
一旦f(n)确定,“我们如何凑出f(n)”就再也用不着了。
要求出f(15),只需要知道f(14),f(10),f(4)的值,而f(14),f(10),f(4)是如何算出来的,对之后的问题没有影响。
“未来与过去无关”,这就是无后效性。
(严格定义:如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。)
步骤划分
刻画一个最优解的结构特征
递归地定义最优解的值
计算最优解的值,通常采用自底向上的方法
利用计算出的信息构造出一个最优解
步骤1~3是动态规划算法求解问题的基础。如果我们仅仅需要一个最优解的值,可以忽略步骤4.如果需要步骤4,有时就需要在步骤3的执行过程中维护一些额外信息,以便用来构造一个最优解。
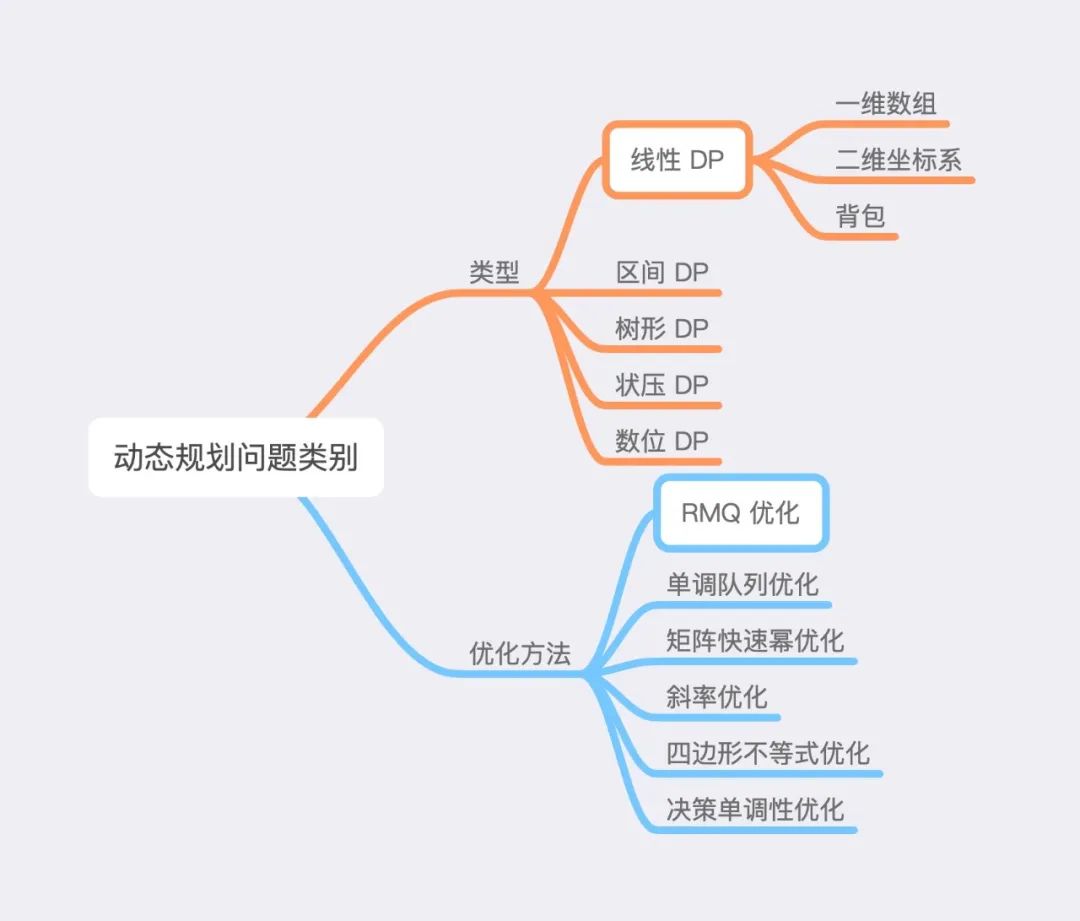
动态规划问题分类
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Sugar Code!